并查集(Union-Find) 判断连通性

2017-12-27 algorithm

有如下的一些点

Points

每次连接其中两个点，然后判断任意两个点是否连通。

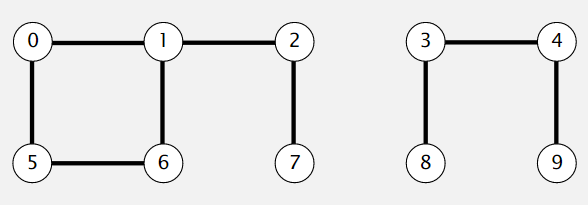
Points

比如上图中的 0 和 1，3 和 9 等等都是连通的，而 2 和 8 不连通。

只有这么一些点，当然好判断，但如果有这么多呢

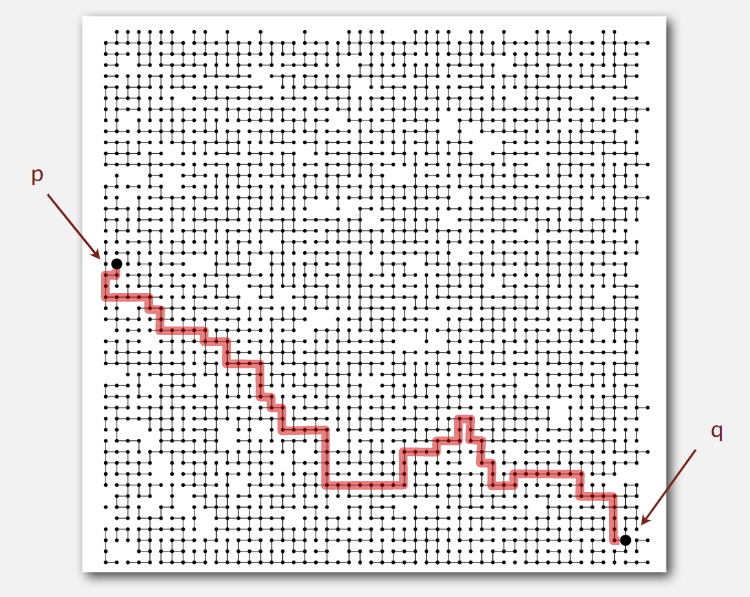
Points

那么，如何通过算法来判断其中两个点是否是连通的呢？

如下图的状态，我们可以将其看作是三个组件(component)。

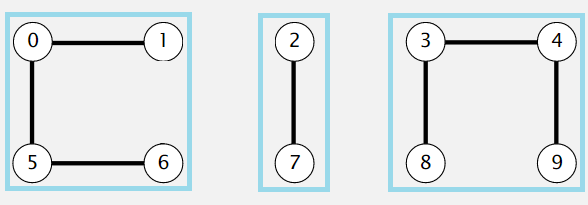
Components

判断两个点是否连通，直接判断它们是否在同一个组件中即可。并为每个组件设置一个 id。

设置一个数组，用来标识这个组件的 id

初始状态下，所有点都是孤立状态，所以它们所在组件的 id 就是它们本身；当两个点被连接后，将其中一个点的_标识_更改为另一个点的_标识_；而当连接两个组件(含一个以上的点)时，可以将其中一个组件中的所有点的标识更改为另一个组件的标识。

当判断两个点是否连接时，直接判断他们是否在同一个组件内。

定义如下的方法

public class UnionFind1 {
    private int[] ids;

    public void union(int p, int q) {
        int pid = ids[p];
        int qid = ids[q];
        for (int i = 0; i < ids.length; i++) {
            // 将所有属于 pid 的组件更换为 qid
            if (pid == ids[i]) {
                ids[i] = qid;
            }
        }
    }
    // 省略其他方法
}

测试一下

UnionFind1 uf = new UnionFind1(10);
uf.union(0, 1);
uf.union(5, 1);
uf.union(6, 5);

uf.union(2, 7);

uf.union(3, 8);
uf.union(4, 9);
uf.union(3, 4);
System.out.println(uf.connected(0, 6));

执行上述操作后

ids 数组的状态如下

ids1

可以看出，0 和 6 属于同一个组件(1)。

但 union() 方法的时间复杂度达到了 O(n)，每次连接两个点，都需要遍历 ids[n]。

这对于少量数据来说还可以，但大量数据就撑不住了。

尝试换一种方式表示一个组件。

将一个组件变为树状的结构，ids[] 数组中的值不再表示所属组件 id，而用来表示这个点的父节点。如下图:

连接状态

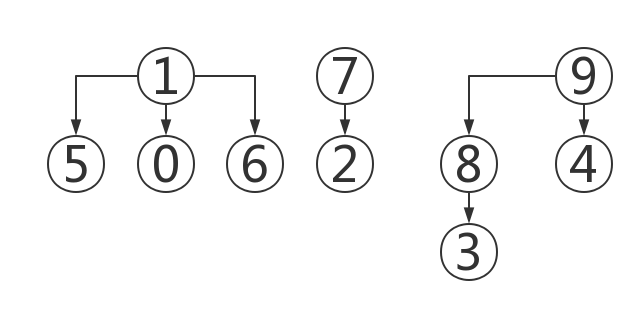
当要连接两个点时，直接将这个点的根节点(如 3 的根节点为 9)指向另一个点的根节点即可。

代码如下

public class UnionFind2 {

    private int[] ids;

    // 获取这个点的根节点
    private int root(int p) {
        while (p != ids[p]) {
            p = ids[p];
        }
        return p;
    }

    public void union(int p, int q) {
        int pid = root(p);
        int qid = root(q);
        ids[pid] = qid;
    }

    public boolean connected(int p, int q) {
        return root(p) == root(q);
    }
}

执行上述的测试后，ids[] 的状态如下

ids2

这样，算法的效率得到了明显的提升。

但。。如果遇到这种情况

uf.union(0, 1);
uf.union(0, 2);
uf.union(0, 3);
// ...

最终，树会变成一个长长的链表，复杂度又变成了 O(n)。

上面导致树变成链表的的原因是，总是将大树接到了小树上。

可以设置一个新的数组 size[n]，用来存放每一颗树的大小，而在进行连接时，总是将较小的树连接到较大的树上。

代码如下

public void union(int p, int q) {
    int pid = root(p);
    int qid = root(q);
    if (size[pid] > size[qid]) {
        ids[qid] = pid;
        size[pid] += size[qid];
    } else {
        ids[pid] = qid;
        size[qid] += size[pid];
    }
}